History and Physical Properties

MathJax.Hub.Config({tex2jax: {inlineMath: [[‚$`‘,’`$‘], [‚\$`‘,’`\$‘]]}});

div.wp-caption img{padding: .5em;}

In 1970 Leon Chua discovered the possibility of a fourth fundamental two-terminal circuit element besides the well-known resistor, inductor and capacitor¹. An implementation of this device would link charge and magnetic flux. What this would imply can be understood when compared to the voltage-current-linkage of the resistor:

Resistor Equation: $`R = \frac{U}{Q / t}`$

Memristor Equation: $`M = \frac{\int_{-\infty}^{t} U(t) dt}{Q}`$

The resistor shows the same units in the end, but is structured differently. While instantaneous voltage in the case of the resistor results in a static behavior for a fixed voltage, the memristor depends on the time integral of the voltage (i.e. the magnetic flux) and therefore changes its “Memristance” over time, even when the voltage stays fixed.

This implies that the memristor has to have some kind of “memory” of the voltage levels it has seen in the past and externalizes this property by its instantaneous resistance.

When we attach a sinusoidal voltage source to a memristor and measure the current flowing through the device we get the famous memristor I-V-hysteresis curve.

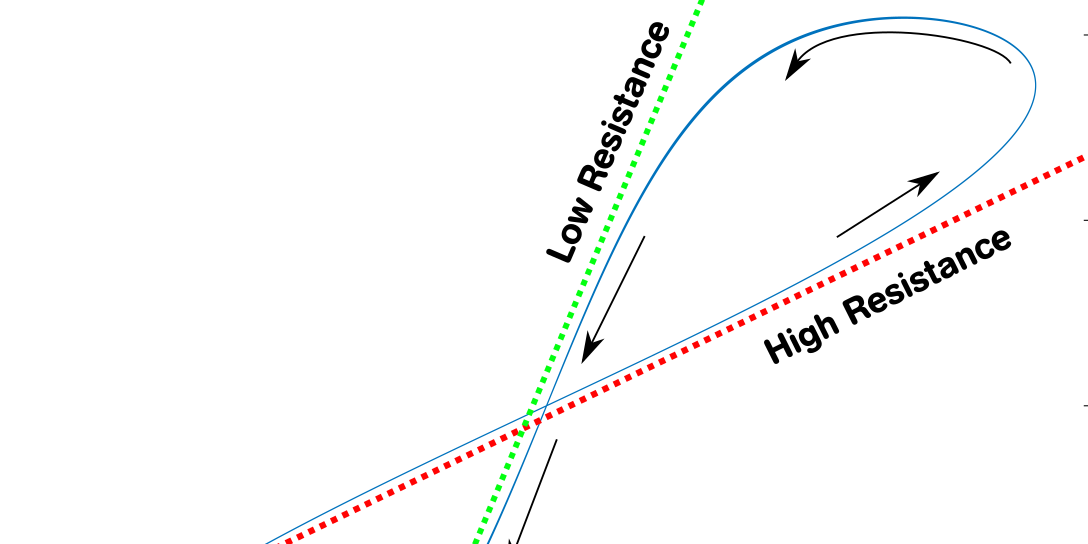
Figure 1: Hysteresis Curve, with Biolek et al. Model

The resistance of a point in the I-V space is determined by the slope of the line going through the point and the origin. A line straight up would be $`0\Omega`$, a diagonal through 1V/1A $`1\Omega`$ and a flat line $`\infty\Omega`$. The picture shows that with a large enough positive voltage the the memristor transitions from a high resistance (red dotted line) to a low resistance (green dotted line). And with the negative voltage the process reverses.

Since Chua’s discovery, multiple devices that adhere to these principles were created, most notably the one developed by the team of the HP Labs. Their device resparked the research interest in memristive technologies.

The HP memristor’s working principle is based on the expansion/contraction of layers of materials with a different conductivity. In practice the chosen material was oxygen-depleted titan-dioxide. The oxygen-depletion makes the remaining oxygen atoms “mobile”, i.e. a voltage can move them in the direction of both electrodes. When this is done, a layer of more conductive, “less oxygen-depleted” material is contracted or expanded.

L. Chua, “Memristor—the missing circuit element.” IEEE Transactions on Circuit Theory, vol. 18(5), pp. 507–519.↩